Khái niệm đồng dạng lượng giác là một khái niệm được sử dụng trong lĩnh vực toán học để chỉ các hàm lượng giác biến đổi có thể được tìm thấy trong một hình hình học. Lượng giác là một nhánh của toán học chuyên phân tích và nghiên cứu các hình tam giác, đặc biệt là về hình dạng, ý nghĩa và giá trị của các góc khác nhau có thể tồn tại. Các nhận dạng lượng giác sau đó sẽ là kết quả của các giá trị đó có thể thay đổi và rất đa dạng từ giá trị này sang giá trị khác.
Cũng như nhiều yếu tố của toán học, các khái niệm đã tồn tại từ thời cổ đại, trong đó các nhà triết học Hy Lạp đã thiết lập các khái niệm về chức năng và giá trị của các góc của các hình hình học. Những khái niệm này sẽ chỉ được cải thiện trong Hiện đại, vào thế kỷ XVII khi chúng được ghi nhận về mặt đại số để có thể thực hiện tất cả các loại phép tính giữa các góc khác nhau.
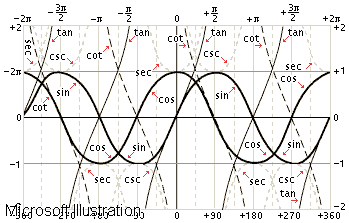
Đồng dạng lượng giác có thể được định nghĩa rộng rãi là tất cả các biến góc có thể có trong một hình hình học. Những danh tính này luôn được thể hiện từ các chữ cái Hy Lạp như alpha, beta, omega, v.v. Các yếu tố như độ bách phân cũng được sử dụng để thiết lập các biến của mỗi danh tính. Những cái được biết đến nhiều nhất là những cái được thiết lập giữa sin và cosine, sin và tiếp tuyến, v.v. Nhận dạng lượng giác là dạng đơn giản cho phép chúng ta thực hiện và biết các chức năng khác nhau của lượng giác. Tất cả những câu hỏi này của toán học, cụ thể hơn là lượng giác, phục vụ cho việc tổ chức các phép tính khác nhau phải được thực hiện từ các hàm cụ thể của từng loại dữ liệu. Các nhận dạng lượng giác rất thay đổi và cho phép có các khả năng khác nhau để biểu diễn mỗi hàm lượng giác (nghĩa là các giá trị) theo những cách khác nhau và cụ thể tùy theo từng trường hợp.
